Sound

What is sound ?

A sound wave is the systematic spread of molecular disruption characterized by the vibration of molecules around their resting position. Following such a disruption, created by a mechanical source, molecules undergo slight pressure variations (known as acoustic pressure) which cause them to come into contact with each other, effectively transmitting the vibration. The displaced molecules return to their starting position once the disruption has passed, meaning that the energy transfer through the medium does not equate to molecular displacement.

Sound waves are successions of molecular compressions and dilations. In this animation, the molecules vibrate around their resting position without displacing.

In this animation, the float moves with the environmental disruption (the waves), but always returns through its starting point. This principle is the same for sound waves: each molecule oscillates around its resting position.

General characteristics

Sounds waves are generally longitudinal, as molecules vibrate in parallel to the direction of the travelling wave. In solids, transverse waves (also known as ‘shear’ waves) also exist.

Furthermore, when the sound wave of a point source propagates in a homogeneous and isotropic environment without obstacles, it does so identically in all directions and is described as ‘spherical’. However, a long way from the sound source, a sound wave can be assimilated into a plane wave, as the wavefront (all of the molecules that vibrate in the same way) tends to be straight.  As a comparison, the planet Earth is round, but on a human scale it appears flat.

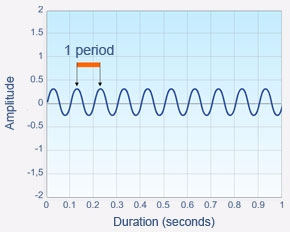
Period

The time interval separating two identical and successive vibratory statesof a single point through which a wave propagates is known as the period, noted T.

This graph represents a wave’s sound pressure variation over a 1 second duration. The period is the time interval between two successive points with the same amplitude. For example, between the 3^rd and 4^th maximum, the period is 0.1 s.

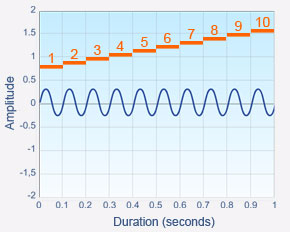
Frequency

Frequency refers to the number of periods by unit of time and corresponds to the inverse of the period: f = 1/T, where f is frequency in Hertz (Hz or s^-1), and T is the period in seconds (s).

In this example, the sinusoid has a period of 0.1 s. The frequency corresponds to the number of periods by second, meaning the number of times that the pattern repeats: 10 times. The frequency is therefore 10 Hz. This number can also be found by calculating the inverse of the period: f = 1/0.1 = 10 Hz.

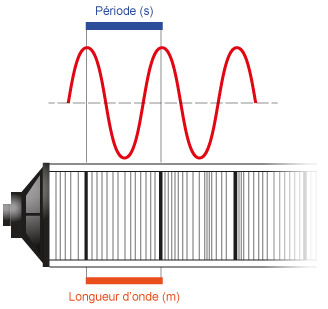
Wavelenth

The distance between two successive molecules in the same vibratory state (the same acoustic pressure and speed) is known as the sound’s wavelength. It is the distance covered by the sound wave during one period.

In this example, the wavelength can be represented by the distance separating two compression maximums (bold lines). At this instant t, each molecule separated by the wavelength is subjected to identical sound pressure and speed.

In a given medium, frequency and wavelength are linked by the formula: λ = v/f = v*T, where λ is the wavelength in metres (m), c is the sound speed in metres per second (m/s), f is frequency (Hz) and T is the period (s). For a sinusoid with a frequency of 10 Hz and a propagation speed of 340 m/s, the wavelength is equal to 34 metres.

Wavelength is inversely proportional to frequency, therefore, the longer a sound’s wavelength, the lower its frequency. Conversely, the shorter the wavelength, the higher the frequency.

Acoustic power

Acoustic, or sound, power, expressed in watts (W) is the energy provided by a sound source in a given time interval. It can be defined by the formula: P=E/Δt, where P is the acoustic power in Watts (W), E is acoustic energy in joules (J), and Δt is an interval of time (s). This variable depends only on the characteristics of the sound source.

Acoustic power has nothing to do with the electrical power of a sound system (such as loudspeakers), which can be many tens of Watt. Electrical power is used to generate acoustic power.

Sound intensity

Sound intensity, expressed in Watt by square metre (W/m²), is the energy which, in each second, travels along a surface perpendicular to a sound wave. In the case of a spherical wave, intensity is linked to power by the formula: I = W/(4*π*r²), where I is the sound intensity (W/m²), W is acoustic power (W), and r is the distance between the source and a measurement point (m). Therefore, the intensity depends not only on the characteristics of the source (via the sound power), but also on the distance of the measurement point from the source.

If the distance of the measurement point from the source doubles, the intensity is divided by 4.

Sound pressure

Sound pressure (p) is applied to the surface of a body. It corresponds to a force per surface unit. In a resting state, molecules are submitted to atmospheric pressure. When the medium is disrupted, the molecular motion causes local variations in pressure: this is sound pressure. Sound pressure and intensity are linked by the formula: I = p²/(ρ*v), where I is the intensity (W/m²), p is sound pressure at a single point expressed in pascal (Pa), ρ is the density of the medium (kg/m³), and c is the propagation speed of the wave (m/s).

Therefore, when sound pressure doubles, acoustic intensity is multiplied by 4.

Duration

Duration depends on the amount of time that the medium is disrupted. It is measured in seconds (s).

The influence of environment on sound

Soundwave propagation speed

When a fluid environment is subjected to compression and dilation, the way it reacts is strictly dependent on the state of the fluid and its elastic properties. Therefore, sound wave propagation speed (known simply as sound speed) depends on certain intrinsic properties of the medium that the wave is crossing: compressibility (the ability to regain its original form after deformation), and density. These two components are influenced by multiple parameters such as temperature, pressure and potential modifications of the medium. The lower these values, the higher the propagation speed of the sound wave will be.

How does this happen in air ?

Temperature

In air, sound speed can be calculated by the formula: c = (331.35 + 0.607 * q), where c is sound speed in air (m/s), and q is the temperature in degrees celcius (ºC). Speed increases with temperature.

In fact, increases in temperature cause decreases in density, as for a given mass, air has more volume. For example, at 0ºC, the density of air is 1.293 kg/m³, and at 20 ºC it is 1.204 kg/m³.

Pressure

For a given temperature, density changes depending on the surrounding pressure. Lower atmospheric pressure equates to lower density as the air dilates. As a result, sound speed increases.

Environmental modification

For a given pressure and temperature, the density of air depends upon the amount of water vapour mixed into the atmosphere. Lower humidity levels give rise to decreases in air density. Therefore, sound velocity is greater when the air is dry than when it is humid.

How does this happen in other mediums  ?

For a temperature of 20°C, a pressure of e1013 hPa, and an absence of relative humidity, the propagation speed of sound in air is around 343 m/s.

In a medium such as water, at a similar temperature of 20°C, a sound wave propagates at 1500m/s, and at even higher speeds in denser mediums (3500 m/s in bone and up to 6000 m/s in iron!). Although these mediums are much denser than air, they are less compressible and stiffer, causing the sound wave to travel quickly through them.

Example: if a sound source is placed under a bell jar, the sound can be heard. However, if a vacuum is created within the bell jar, the sound disappears as there are no longer any air molecules present to propagate the sound.

Acoustic impedance

Each medium is characterised by a resistance known as ‘acoustic impedance’. Generally, it corresponds to the ratio between the acoustic pressure at a given point and the vibration speed of the molecules at that point (this should not be confused with sound speed).

In the case of a plane wave, the impedance can be estimated by the formula: Z= ρ*c, where Z is the characteristic acoustic impedance of the medium (Pa.s/m), ρ is the density of the medium (kg/m³) and sound speed (m/s).

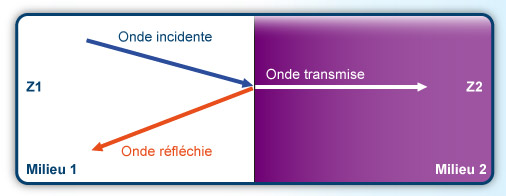
The impedance of air is therefore around 444 Pa.m/s, and that of water 1.5*106 Pa.m/s, or a ratio of 304*10³. This is an important notion for understanding the reaction of a sound wave propagating in air compared to liquid. Upon contact with the higher-impedance medium, a large part of the wave is reflected.

The characteristics of impedance are used in numerous fields, including oceanography (sonar), medical imaging, and construction (e.g. to test the quality of cement by estimating the amount of air contained within it). By altering the impedance of a medium, the passage of a sound wave can also be facilitated: an example comes from our ears (see ‘The Ear’).

An example of impedance adaptation: in echography, a probe placed on a patient’s skin emits ultrasounds. However, the smallest pocket of air between the skin and the probe can cause attenuation of the signal. This is due to the fact that the impedance of air and that of skin are very different – that of skin is 10000x greater. By applying a gel with similar impedance to that of skin, the presence of air molecules is limited and the passage of ultrasounds is optimised.