Son : généralités
Conception : Antoine Lorenzi Benjamin Chaix
Avec la participation de : Joël Ducourneau
Le son est une onde produite par une vibration mécanique du support, ou milieu, pouvant être solide, liquide ou gazeux.
Par anthropomorphisme, on peut définir le son comme représentant la partie audible du spectre des vibrations acoustiques, de même que la lumière se définit comme la partie visible du spectre des vibrations électromagnétiques.
Qu’est-ce qu’un son ?
Une onde sonore est la propagation de proche en proche d’une perturbation caractérisée par une vibration des molécules du milieu autour de leurs positions d’équilibre (ou état de repos). En effet, suite à une perturbation, créée à l’origine par une source mécanique, les molécules subissent de faibles variations de pression (pression acoustique) ; elles s’entrechoquent entre elles pour transmettre la déformation (perturbation) subissant ainsi de micro-déplacements. Ces molécules reviennent à leur position initiale une fois la perturbation passée ; c’est une propagation d’énergie dans un milieu matériel sans transport de matière.
Une onde sonore est une succession de compressions / dilatations des molécules. Sur cette animation, on voit que les molécules vibrent autour de leur position d’équilibre et qu’elles ne se déplacent guère, ou de quelques micromètres.
Cette animation montre que le flotteur (bouchon) se déplace au gré des perturbations (vagues) mais repasse toujours par sa position d’origine. C’est le même principe pour les ondes sonores : chaque molécule oscille autour de sa position d’équilibre.
Caractéristiques générales
Une onde sonore est le plus souvent une onde mécanique longitudinale, car les molécules se déplacent parallèlement au sens de propagation de l’onde. Dans les solides, il peut également exister des composantes transversales.
De plus, lorsqu’elle évolue dans un milieu homogène, isotrope et sans obstacle, l’onde d’une source idéale se propage de manière identique dans toutes les directions, elle est dite sphérique. Cependant, à une distance importante de la source, l’onde sonore peut être assimilée à une onde plane car le front d’onde (ensemble des molécules qui oscillent dans le même état vibratoire) tend à être rectiligne. A titre de comparaison, la planète Terre est ronde mais à l’échelle humaine, elle est plane.
Période
La période, notée T, est l’intervalle de temps séparant deux états vibratoires identiques et successifs d’un point du milieu dans lequel l’onde se propage.
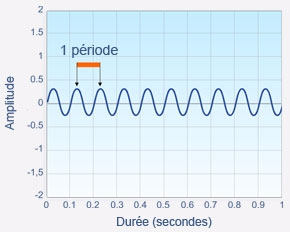
La période, notée T, est l’intervalle de temps séparant deux états vibratoires identiques et successifs d’un point du milieu dans lequel l’onde se propage.
Longueur d’onde
La longueur d’onde est la distance séparant deux molécules successives dans le même état vibratoire (même pression et vitesse acoustique) ou encore la distance parcourue par l’onde pendant une période.
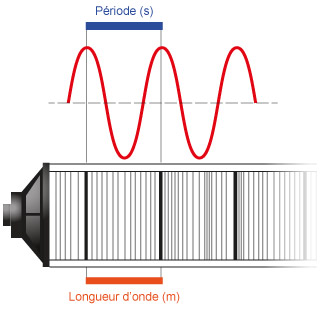
Dans l’exemple choisi ici, la longueur d’onde peut être représentée comme la distance séparant deux maximums de compression (traits gras successifs) ; à cet instant t, chaque molécule séparée de la longueur d’onde est soumise à une pression et une vitesse acoustiques identiques.
Dans un milieu donné, la fréquence et la longueur d’onde sont liées par la formule : λ=c/f=c*T ou λ est la longueur d’onde en mètre (m), c la célérité de propagation de l’onde en mètre par seconde (m.s-1), f la fréquence (Hz) et T la période (s). Pour une sinusoïde de fréquence 10 Hz et une célérité de propagation de l’onde égale à 340 m.s-1, la longueur d’onde vaut 34 mètres.
Plus la longueur d’onde est grande, plus la fréquence est faible. A l’inverse, plus elle est faible, plus la fréquence est élevée.
Puissance acoustique
Exprimée en watt, la puissance acoustique est l’énergie délivrée par une source sonore pendant un intervalle de temps donné. Elle peut être définie par la formule : P=E/Δt ou P est la puissance acoustique en Watt (W), E l’énergie acoustique en joules (J), et Δt un intervalle de temps (s). Cette variable dépend uniquement des caractéristiques de la source.
Attention, elle n’a rien à voir avec la puissance électrique d’un système sonore (des enceintes par exemple) qui est, parfois, de plusieurs dizaines de Watt. La puissance électrique va permettre de générer une puissance acoustique.
Intensité acoustique (ou puissance surfacique)
Exprimée en Watt par mètre carré, (W.m-2), l’intensité acoustique correspond à l’énergie qui traverse chaque seconde une surface unitaire perpendiculaire à la direction des ondes sonores. Dans le cas d’une source d’ondes sphériques, elle est liée à la puissance par la formule : I=W/(4*π*r²) ou I est l’intensité acoustique (W.m-2), W la puissance acoustique (W) et r la distance entre la source et un point de mesure (m). Ainsi, l’intensité dépend non seulement des caractéristiques de la source par le biais de la puissance mais également de la distance du point de mesure par rapport à la source.
Si la distance du point de mesure par rapport à la source double, l’intensité sera divisée par 4.
Pression acoustique
La pression p est une contrainte appliquée à la surface d’un corps. Elle correspond à une force par unité de surface. Au repos, les molécules sont soumises à la pression atmosphérique. Lorsque le milieu est perturbé, le mouvement des molécules engendre des variations locales de la pression ; c’est la pression acoustique. La pression et l’intensité acoustique sont liées par la formule : I=p²/(ρ*c) ou I est l’intensité (W.m-2), p la pression acoustique en un point exprimée en Pascal (Pa), ρ la masse volumique du milieu (kg.m-3), c la célérité de propagation de l’onde (m.s-1).
Ainsi lorsque la pression est deux fois plus forte, l’intensité acoustique multipliée par 4.
Durée
Elle dépend du temps pendant lequel le milieu est perturbé. L’unité utilisée est la seconde (s).
Influence du milieu sur le son
Vitesse de propagation de l’onde : la célérité du son
Les réactions d’un fluide (milieu) soumis à des pressions et des dilatations sont étroitement dépendantes des états du fluide et de ses propriétés élastiques. L’onde acoustique se propage donc à des vitesses différentes en fonction de certaines caractéristiques intrinsèques du milieu qu’elle traverse : la compressibilité (c’est-à-dire l’aptitude à reprendre la forme originale après déformation) et la masse volumique. Ces deux composantes sont influencées par plusieurs paramètres tels que la température, la pression et d’éventuelles modifications du milieu. Plus ces deux composantes seront faibles, plus la vitesse de propagation de l’onde qu’on appelle célérité sera importante. La masse volumique est, par exemple, influencée par la température, la pression et d’éventuelles modifications du milieu.
Température
Dans l’air, la célérité du son peut être approximée par la formule : c=(331,35+ 0,607*q) ou c est la célérité du son dans l’air (m.s-1) et q la température en degré Celsius. Plus la température augmente, plus la vitesse de propagation augmente.
En effet, plus la température augmente, plus la masse volumique diminue car pour une masse donnée, l’air est plus volumineux. Ex. à 0°C, la masse volumique de l’air est de 1,293 kg.m-3, et à 20°C de 1,204 kg.m-3.
Pression
Pour une température donnée, la pression à laquelle est soumis l’air modifie sa masse volumique. Moins la pression est forte, moins la masse volumique est importante car l’air se dilate. Par extension, la célérité du son augmente.
Modification du milieu
Pour une pression et une température donnée, la vapeur d’eau qui peut se mélanger à l’air à un impact sur la masse volumique de ce dernier. Moins l’humidité relative sera importante, moins la masse volumique de « l’air » le sera. Ainsi, le son se propagera plus rapidement dans l’air sec qu’humide.
Comment cela se passe-t-il dans d’autres milieux ?
Pour une température de 20°C, une pression de 1013 hPa et une humidité relative nulle, la vitesse de propagation de l’onde sonore dans l’air est d’environ 343m.s-1.
Dans un milieu tel que l’eau, à une température ambiante de 20°C, une onde sonore se propage à 1500 m.s-1 et à des vitesses encore supérieures dans les matériaux plus denses (3500 m.s-1 dans l’os et jusqu’à 6000 m.s-1 dans l’acier !). En effet, même si ces matériaux ont une masse volumique plus importante que l’air, leur coefficient de compressibilité est très faible. Ainsi, l’onde sonore s’y propage rapidement.
Dans le vide, dépourvu de matière, aucune onde sonore ne se propage (le milieu doit être constitué de matière), à l’inverse des ondes électromagnétiques qui peuvent s’y propager.
Exemple : si on met une source sonore sous une cloche, on entend le son. En revanche, si on fait le vide sous la cloche, le son disparait puisqu’il n’y a plus de molécules d’air.
Impédance acoustique
Pour une température de 20°C, une pression de 1013 hPa et une humidité relative nulle, la vitesse de propagation de l’onde sonore dans l’air est d’environ 343m.s-1.
Dans un milieu tel que l’eau, à une température ambiante de 20°C, une onde sonore se propage à 1500 m.s-1 et à des vitesses encore supérieures dans les matériaux plus denses (3500 m.s-1 dans l’os et jusqu’à 6000 m.s-1 dans l’acier !). En effet, même si ces matériaux ont une masse volumique plus importante que l’air, leur coefficient de compressibilité est très faible. Ainsi, l’onde sonore s’y propage rapidement.
Dans le vide, dépourvu de matière, aucune onde sonore ne se propage (le milieu doit être constitué de matière), à l’inverse des ondes électromagnétiques qui peuvent s’y propager.
Exemple : si on met une source sonore sous une cloche, on entend le son. En revanche, si on fait le vide sous la cloche, le son disparait puisqu’il n’y a plus de molécules d’air.
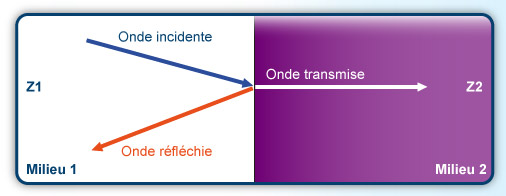
Ainsi, l’impédance de l’air est d’environ 444 kg. m-2.s-1 et celle de l’eau de 1,5*106 kg. m-2.s-1 soit un rapport de 3,4*103. Cette notion est importante pour comprendre la réaction d’une onde sonore se propageant d’un milieu aérien vers un milieu liquidien. Au contact du milieu d’impédance élevée une partie importante de l’onde sera réfléchie.
Ces caractéristiques d’impédance sont utilisées dans divers domaines, l’océanographie (sonar), l’imagerie médicale, ou encore le bâtiment pour tester par exemple la qualité du béton en estimant la concentration de bulle d’air qui le constitue. On peut également favoriser le passage d’une onde d’un milieu à un autre en adaptant l’impédance, c’est ce que fait par exemple notre oreille (Voir Fonctionnement oreille).
Exemple d’adaptation d’impédance: En échographie, une sonde appliquée sur la peau du patient émet des ultrasons. Or, même une fine pellicule d’air entre la sonde et la peau peut entraîner une atténuation du signal. En effet, les impédances de l’air et la peau sont très différentes, celle de la peau étant 10000 fois plus importante. En appliquant un gel dont l’impédance est proche de celle de la peau on limite d’une part la présence d’air et optimise le passage des ultrasons.