Représentation du son
Conception : Antoine Lorenzi Benjamin Chaix
L’étude du son a donné naissance à différents modèles de représentations ayant chacun un intérêt particulier.
Les modes de représentation du son
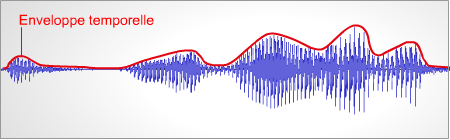
Représentation temporelle
Cette représentation montre l’évolution de l’intensité du signal sonore dans le temps.
La partie en bleu montre l’évolution de l’intensité d’un son de parole dans le temps. Cette vue temporelle permet notamment d’apprécier l’évolution de l’enveloppe temporelle (ligne rouge) qui, par exemple, joue un rôle important dans la perception de la parole.
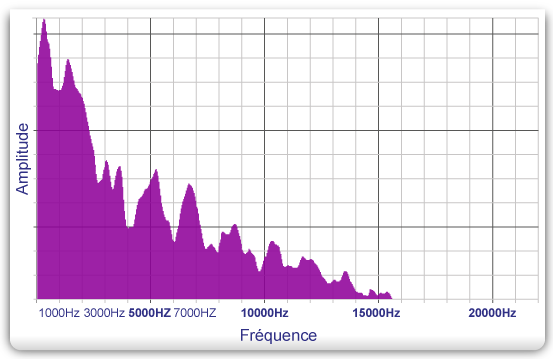
Représentation fréquentielle (ou spectrale)
Ce mode permet de visualiser la composition fréquentielle d’un son mais également l’intensité de chaque fréquence.
Sur ce graphe, on peut voir la composition spectrale de l’échantillon sonore précédent. On peut ainsi voir dans cet exemple que les fréquences du son choisi s’étendent de 80 Hz à 15500 Hz.
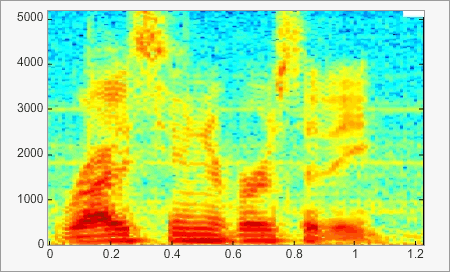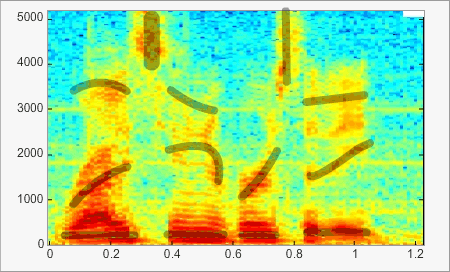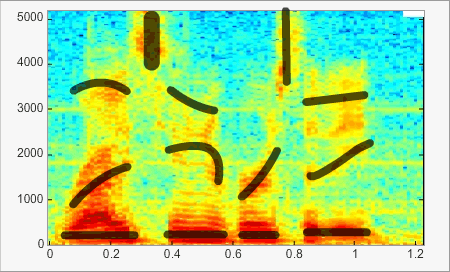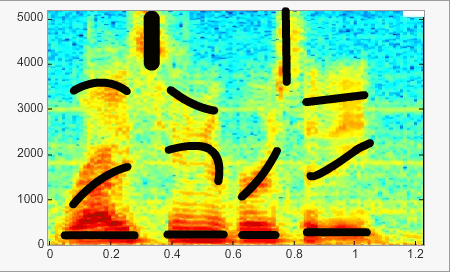
Représentation tridimensionnelle : le sonagramme ou spectrogramme
Il s’agit de la représentation temps-fréquence du son. On trace la répartition énergétique du son en fonction du temps et des fréquences. Le sonagramme est très utilisé pour étudier le signal de parole.
L’exemple ci-dessus montre bien l’évolution de la fréquence et de l’intensité dans le temps. L’intensité est définie par la couleur : plus la couleur évolue vers le rouge plus l’intensité est importante. Les trait noirs soulignent les formants des voyelles, les transitoires formantiques, …
Quelques sons courants
Parole

Spectre réel du mot « cochlée ». Les voyelles sont représentées par des groupes de raies qui émergent du spectre et sont appelés « formants ».
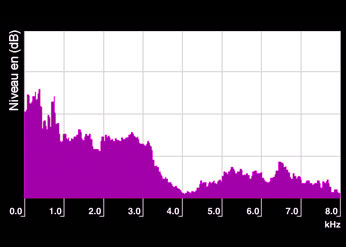
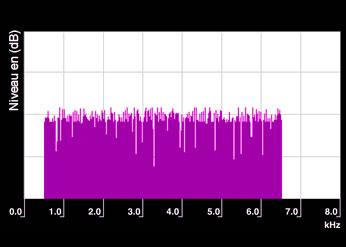
Bruit blanc

Spectre théorique d’un bruit blanc qui a été limité à la bande de fréquence 500-6500 Hz. Le bruit blanc étant continu et formé par un « continuum » de fréquences, il n’est pas possible d’individualiser des raies spectrales.
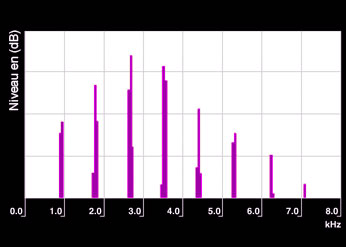
Son musical

Spectre réel d’un son musical comprenant un fondamental à 880 Hz (note la 4) et 7 harmoniques dont les fréquences sont des multiples entiers de la fréquence fondamentale. Comme pour le son pur, les raies spectrales sont plus larges que ne le prévoit la théorie.
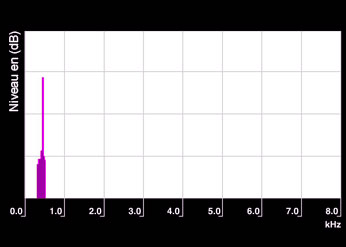
Son pur

Spectre réel d’un son pur de fréquence 440 Hz obtenu avec un analyseur de spectre. La raie spectrale réelle est toujours plus large que ne le prévoit la théorie.
Échelle des Bels
La plus faible intensité à laquelle est sensible l’oreille humaine est, en moyenne, de 10-12 W.m-2 et la plus forte environ 1 W.m-2 soit un rapport de mille milliards entre les deux. Cette échelle n’étant pas facile à utiliser, elle a été transcrite en Bels. Ceux-ci sont basés sur un système logarithmique d’évaluation relative, c’est-à-dire le rapport entre deux grandeurs de même espèce.
Par exemple, pour évaluer le niveau d’intensité acoustique, la valeur référence sera la plus petite intensité à laquelle est sensible l’oreille humaine soit comme dit auparavant : I = 10-12 W.m-2. Si on veut savoir à quel niveau correspond I1 = 1 W.m-2, il suffit donc de faire le logarithme du rapport entre I1 et I : Niveau d’intensité = log10(I1/I ) = log10(1012) = 12 bels.
En ajoutant un facteur multiplicateur de 10, on obtient une échelle exprimée en décibels (dB) qui correspond à celle de la sonie (sensation subjective d’intensité sonore). Ainsi une intensité de 1 W.m-2 correspond à un niveau d’intensité acoustique de 120 décibels.
LI = 10.log10(I1/I ). Si l’intensité acoustique est doublée, le niveau sonore est multiplié par 2 (soit une augmentation de +3 dB)
Lorsque on évalue le niveau de pression acoustique, l’unité décibel est souvent succédée des lettres SPL (« Sound Pressure Level ») qui caractérisent la pression acoustique de référence p0 = 20*10-6 Pa = 20 mPa (pression acoustique minimale à laquelle est sensible l’oreille).
Comme indiqué précédemment, l’intensité acoustique est proportionnelle à la pression acoustique p au carré. Ainsi le niveau de pression acoustique est défini par la relation suivante : LSPL = 20.log10(p/p0). Si la pression acoustique p est doublée, le niveau sonore est multiplié par 4 (soit une augmentation de +6 dB).
Les seuils d’audition sont exprimés en décibels de perte, le dB HL (hearing loss). Cette échelle tient compte des différentes sensibilités de l’oreille en fonction des fréquences sonores. A titre d’exemple, une personne normo-entendante détecte un son de 500Hz à partir de 10dB SPL, un son de 2000Hz à partir de 0dB SPL et un son de 8000Hz à partir de 20dB SPL. A des fins audiologiques ces seuils d’audition aux différentes fréquences audibles sont ramenés à 0dB HL. Un audiogramme permet donc de représenter les seuils d’audition par rapport à une référence établie sur une large population normo-entendante. Ainsi, on peut classer différents degrés de surdité grâce à cette échelle (voir la partie audiométrie tonale).